整除/gcd

设a,b两个整数，如果存在整数$c$使得$a=bc$，则称$b$整除$a$，又称$a$是$b$的倍数，$b$是$a$的因子,记作$a|b$.
设两个整数a,b，且$b\ne 0$，则存在唯一的整数$q$和$r$使得
$$
a = qb + r, 0 \le r < |b|
$$

整数相关性质

性质1:
$$
a | c, b | c \Rightarrow ab | c
$$
性质2:
$$
a | b, b | c \Rightarrow a | c
$$
性质3:
设$m \ne 0$，则
$$
a | b \Rightarrow ma | mb
$$
性质4:
$$
若a | b, b | a \Rightarrow a = \pm b
$$

素数/合数

应该没人不知道什么是素数
pass

不知道该叫什么定理

合数$m$的最小的不等于 1 的正因子$p$一定是素数,且$p \le \sqrt{m}$.

伯特兰-切比雪夫定理

设整数$n > 3$，至少存在一个素数$p$满足$n < p < 2 * n - 2$.
证明略，有兴趣可以自己搜

算数基本定理

设$a > 1$，则
$$
n=p_1^{r_1}p_2^{r_2}p_3^{r_3}…p_k^{r_k}
$$
其中$p_1,p_2,p_3,…,p_k$是不相同的质数，$r_1,r_2,r_3,…,r_k$是正整数，且在不计顺序的情况下该表示是唯一的

定理中的表达式叫做a的质因数分解

证明
首先用数学归纳法证明𝑛可以分解成一些素数的乘积。
当𝑛 = 2时，因为 2 是素数，结论成立。
假设小于𝑛且大于 1 的整数都可以分解成一些素数的乘积.
对于$n$，$n$是素数则结论成立。否则，若$n$是一个合数，$n$存在最小正素因子𝑝1，设$n=p_{1}n_{1}$，则$1<n_{1}<n$，根据归纳假设，𝑛1可以分解成一些素数的乘积，不妨设$n_{1}=p_{2}p_{3}…p_{s}$可得$n=p_{1}p_{2}p_{3}…p_{s}$
接着利用反证法证明分解的唯一性

公约数、公倍数

设$a,b$是两个整数，如果$d|a$且$d|b$，则称$d$为$a$和$b$的公因子或公约数，
其中最大的称作最大公约数记作$gcd(a,b)$
设$a,b$是两个整数，如果$a|d$且$b|d$，则称$d$为$a$和$b$的公倍数，
其中最小的称作最小公倍数记作$lcm(a,b)$

欧几里得算法求gcd

1
2
3
int gcd(int a, int b) {
    return !b ? a : gcd(b, a % b);
}

$lcm(a,b) = ab / gcd(a,b)$

裴蜀定理

设$a,b$是不全为$0$的整数，则存在整数$x,y$使得$ax+by=gcd(a,b)$

给出大致证明

  1. 如果$a,b$中有0，显然成立
  2. $a,b \ne 0$。
    由于$gcd(a,b) = gcd(a, -b)$，不妨设$a,b > 0,且a \ge b, gcd(a,b)=d$
    对$ax+by=d$两边同时除以$d$，可得$a_1x+b_1y=1$，其中$(a_1,b_1) = 1$
    现在只需要证$a_1x+b_1y=1$
    回顾$gcd(a,b)$，$gcd(a,b) \Rightarrow gcd(b, a mod b) \Rightarrow …$
    $$
    gcd(a_1,b_1) = gcd(b_1, r_1) = gcd(r_1, r_2) = … = (r_{n-1}, r_n) = 1
    $$
    到了$(r_{n-1},r_n)$互质的时候开始往回推，消去$r_1~r_{n-2}$，就可以证得$1=a1+b1y$

扩展欧几里得

常用于求 $ax+by=\gcd(a,b)$ 的一组可行解。
然后根据该方程的等式关系进行参数变换

1
2
3
4
5
6
7
8
9
10
11
int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

同余

什么是同余？
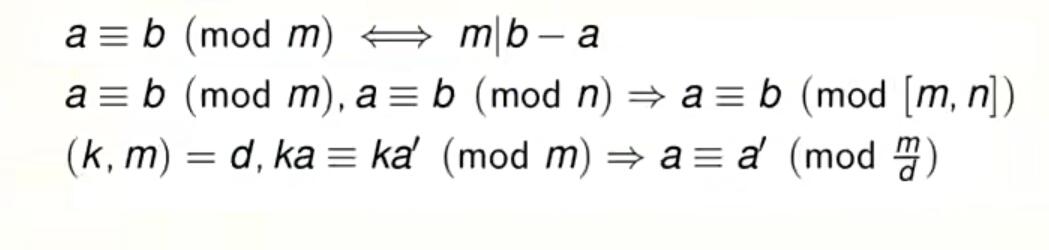
QQ截图20230912203158.jpg

欧拉定理

设$m$为正整数，$gcd(a, m) = 1$，那么$a^{\varphi (m)} \equiv 1(mod m)$
证明比较麻烦，涉及到比较的概念，可以看看相关教材

线性同余方程

形如$ax\equiv b\pmod n$的方程称为线性同余方程。其中，$a、b$ 和 $n$ 为给定整数，$x$ 为未知数。需要从区间 $[0, n-1]$ 中求解 $x$，当解不唯一时需要求出全体解。

扩展欧几里得求解

方程可变为$ax-my=b$,扩欧求$x$即可

逆元求解

什么是逆元？
如果一个线性同余方程 $ax \equiv 1 \pmod b$，则 x 称为 $a \bmod b$ 的逆元，记作 $a^{-1}$

  • 求逆元
    1. 扩展欧几里得，原理和扩欧求线性同余方程一样
    2. 快速幂法：依赖于费马小定理 $x \equiv a^{b-2} \pmod b$。
  • 线性求n个数逆元—利用逆元性质公式转化
    1
    2
    3
    4
    5
    s[0] = 1;
    for (int i = 1; i <= n; ++i) s[i] = s[i - 1] * a[i] % p;
    sv[n] = qpow(s[n], p - 2);
    for (int i = n; i >= 1; --i) sv[i - 1] = sv[i] * a[i] % p;
    for (int i = 1; i <= n; ++i) inv[i] = sv[i] * s[i - 1] % p;

来到例题小凯的疑惑

筛

埃氏筛

1
2
3
4
5
6
7
8
9
10
11
12
13
int primes[N], cnt;
bool st[N];

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

线性筛

只被筛一次，被最小质因数筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int primes[N], cnt;
bool st[N];

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

欧拉函数

欧拉函数，即 $\varphi(n)$，表示的是小于等于$ n $和$ n $互质的数的个数。
比如说 $\varphi(1) = 1$。
当$ n $是质数的时候，显然有$ \varphi(n) = n - 1$。

1
2
3
4
5
6
7
8
9
10
11
12
13
int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);

    return res;
}

利用筛求欧拉函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int primes[N], cnt;
int euler[N];
bool st[N];

void euler_(int n)
{
    euler[1] = 1;
    for(int i=2;i<=n;i++)
    {
        if(!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
         for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}

中国剩余定理(CRT)

中国剩余定理可求解如下形式的一元线性同余方程组$（其中 n_1, n_2, \cdots, n_k 两两互质$）：
$$
\begin{cases}
x \equiv a_1 \pmod {n_1} \
x \equiv a_2 \pmod {n_2} \
… \
x \equiv a_k \pmod {n_k} \
\end{cases}
$$
模$M=n_{1}n_{2}…n_{k}$有唯一解
$$
x \equiv \sum_{i=1}^{k}a_{i}\tfrac{M}{n_{i}}(\mod n_{i})\pmod M
$$

证明
存在性:
若
$$
x \equiv \sum_{i=1}^{k}a_{i}\tfrac{M}{n_{i}}\left ( \frac{M}{n_{i}}\right )^{-1}(\mod n_{i})\pmod M
$$
对任意$1 \le j \le k$,有
$$
x \equiv \sum_{i=1}^{k}a_{i}\tfrac{M}{n_{i}}\left ( \frac{M}{n_{i}}\right )^{-1}(\mod n_{i})(\mod n_{j})
$$
因为$n_{1},n_{2},…,n_{k}$两两互质，所以当$i = j$时,$gcd(\frac{M}{n_{i}}, n_{j}) = 1$
$$
a_{i}\tfrac{M}{n_{i}}\left ( \frac{M}{n_{i}}\right )^{-1}(mod n_{i}) \equiv a_{i} (mod n_{k})
$$
当$i \ne j$，$gcd(\frac{M}{n_{i}}, n_{j}) = n_{j}$
$$
a_{i}\tfrac{M}{n_{i}}\left ( \frac{M}{n_{i}}\right )^{-1}(mod n_{i}) \equiv 0 (mod n_{k})
$$
故，存在性得证。

唯一性:不会

求解过程:按照定理内容模拟就是
计算所有模数的积$M$；
对于第 i 个方程：
计算 $m_i=\frac{M}{n_i}$
计算 $m_i $在模 $n_i$ 意义下的逆元 $m_i^{-1}$
计算 $c_i=m_i^{-1}$（不要对 n_i 取模）。
方程组在模 $M$ 意义下的唯一解为：$x=\sum_{i=1}^k a_ic_i \pmod n$。

1
2
3
4
5
6
7
8
9
10
LL CRT(int k, LL* a, LL* r) {
  LL n = 1, ans = 0;
  for (int i = 1; i <= k; i++) n = n * r[i];
  for (int i = 1; i <= k; i++) {
    LL m = n / r[i], b, y;
    exgcd(m, r[i], b, y);  // b * m mod r[i] = 1
    ans = (ans + a[i] * m * b % n) % n;
  }
  return (ans % n + n) % n;
}

数论分块

数论分块，又叫整除分块，数论分块可以快速计算一些含有除法向下取整的和式（即形如 $\sum_{i=1}^nf(i)g(\left\lfloor\dfrac ni\right\rfloor)$ 的和式）。当可以在$ O(1) $内计算$ f(r)-f(l) $或已经预处理出 f 的前缀和时，数论分块就可以在 $O(\sqrt n) $的时间内计算上述和式的值。

给出一个结论，给定一个整数$n$，则对于$\left\lfloor\dfrac ni\right\rfloor$，$i$属于正整数且小于$n$，有$2\sqrt n$种取值

用数学语言表示就是
$$
\forall n \in \mathbb{N}{+}, \left|\left{ \lfloor \frac{n}{d} \rfloor \mid d \in \mathbb{N}{+},d\leq n \right}\right| \leq \lfloor 2\sqrt{n} \rfloor
$$

这也表示对于$\left\lfloor\dfrac ni\right\rfloor$ 的结果可以分成值相同的一段段，从而完成快速求和，这就是数论分块

1
2
3
4
5
6
for(int l = 1; l <= n; l++)
{
    int d = n / l, r = n / d;
    // 表示[l,r]这一段 n / x 都 == d
    l = r;
}

如何快速求和UVa11526 H(n)

1
2
3
4
5
6
for(int l = 1; l <= n; l++)
{
    int d = n / l, r = n / d;
    sum += (r - l + 1) * d;
    l = r;
}

给出一道最近遇到的数论分块Small Products

大致题意
求长度为$K$的序列中，由正整数组成，且任意两个相邻元素的乘积最多为$N$，模数为 $10^{9}+7$ 的序列个数。

首先，长度为$K$的序列和任意两个相邻元素的乘积，如果前面确定了一个数$x(x < n)$，后面接着的数必然是$\le \left\lfloor\dfrac {n}{x}\right\rfloor$，然后往后面递推，可用前缀和优化
$$
dp_{i,j} = \sum {x=1} ^{\left\lfloor\dfrac {n}{j}\right\rfloor} f{i-1,x}
$$
时间复杂度$O(NK)$
这么做肯定不行，既然说了要用数论分块，肯定是对$\left\lfloor\dfrac {n}{j}\right\rfloor$下手

考虑 $\left\lfloor\dfrac {n}{x}\right\rfloor = \left\lfloor\dfrac {n}{y}\right\rfloor = t, x \ne y$，
则$dp_{i,x} = dp_{i,y} = \sum {j=1} ^{t} dp{i-1, j}$，这就说明在一个整除块$\left\lfloor\dfrac {n}{j}\right\rfloor$内,$dp_{i}{j}$相等，我们就可以用数论分块加快计算
$$
​ dp_{i,j} = \sum {x=1} ^{cnt} dp{i-1,块的下标} * len_{x}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
#define int long long
int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-') f = -1;
        ch = getchar();
    } 
    while(ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int n, tot, k, cnt[100010], len[100010];
int dp[110][100010];
const int mod = 1e9 + 7;

signed main()
{
    int n = read(), k = read();
    map<int, int> mp;
    for(int l = 1; l <= n; l++)
    {
        int d = n / l, r = n / d;
        cnt[++tot] = r;
        mp[r] = tot; // r对应的块的下表
        len[tot] = r - l + 1;
        l = r;
    }
    for(int i = 1; i <= tot; i++ ) dp[0][i] = 1;
    for(int i = 1; i <= k; i++)
        for(int j = 1; j <= tot; j++)
        {
            dp[i][j] = (dp[i][j - 1] + len[j] * dp[i - 1][mp[n / cnt[j]]]) % mod;
        }
        cout << dp[k][tot];
    return 0;
}

然后来一点简单点的例题()