离散数学
数理逻辑
数理逻辑也叫符号逻辑，用数学的方法从量的侧面来研究推理的规律。同时，引入了一套符号体系，时研究符号化、形式化的逻辑演绎规律的数学分支。其中逻辑验算、谓词演算是其最基础的内容。
古典/形式逻辑
亚里士多德的三段论：所有人都是要死的，苏格拉底是人，因此苏格拉底是要死的。
古典逻辑分析语言所表达的逻辑维形式，但自然语言中含糊不清不易判别的语句会引起歧义，甚至争论。
命题符号化 ：数理逻辑最早的萌芽。由莱布尼茨提出，用数学符号式的“通用语言”来进行思维演算，使人们能够证明思维的正确性，从而避免争论。
布尔代数 ：一种思维的代数，初步实现了莱布尼茨的部分设想。
命题逻辑/命题演算 ：布尔代数发展为具有逻辑蕴含式的命题演算，有最简单的公理化的逻辑系统。
谓词符号化 ：由德摩根提出，使数学中的“关系”、“函数”都可以在逻辑命题中出现，加强了逻辑的表现力。
谓词演算 ：公理化的谓词演算是谓词逻辑的基础。
以上就是命题逻辑的发展过程。
数理逻辑需要用语言来表达概念、陈述理论规则，自然语言不够确切，容易产生二义性，于是诞生了目标语言，如单条件蕴含：→，和蕴含关系，如 ⇔。
命题
真值与分类
命题 就是能够判明真假的陈述句，在命题逻辑中，对命题的成分不再细分，因而命题就成了命题逻辑中最基本也是最小的研究单位。
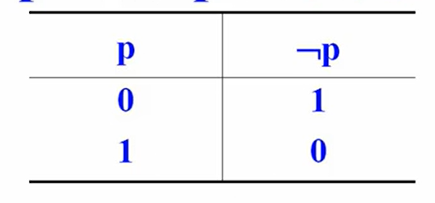
真值 是命题的判断结果，真值只有真和假两种用 T 和 F 或者 1 和 0 表示。任何命题的真值都是唯一的。真值为真的命题成为真命题，表示命题表达的判断正确，真值为假的命题称为假命题，表示命题表达的判断错误。
例子
- 多美丽的景色啊！ 不是陈述句故不是命题。
- 你喜欢大学生活吗？ 不是陈述句故不是命题。
- 3+2=5 真命题。
- 3+2=1 假命题。
- x+2=5 不是命题。
- 郑州是河北省会。 真命题。
- 我在说谎。 悖论。
原子命题/简单命题 是简单得不能再分解的陈述句。反映了对单一事物真假判定，通常用(带下标的)大写字母和数字表示。
复合命题 就是原子命题通过逻辑联结词组合成新的命题。
对于复合命题，无论组成它的原子命题是何取值结果都为假，称之为矛盾式也叫永假式，反之称为重言式也叫永真式。
命题联结词
否定联结词
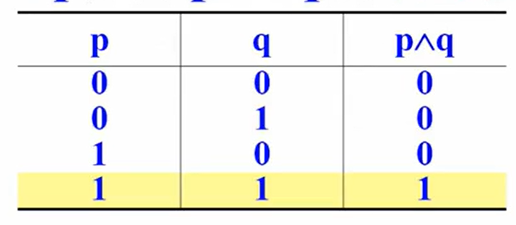
合取联结词
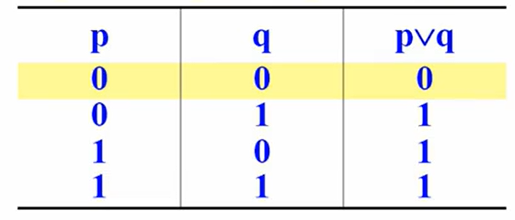
析取联结词
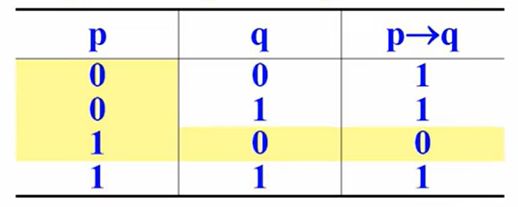
蕴含联结词
等价联结词
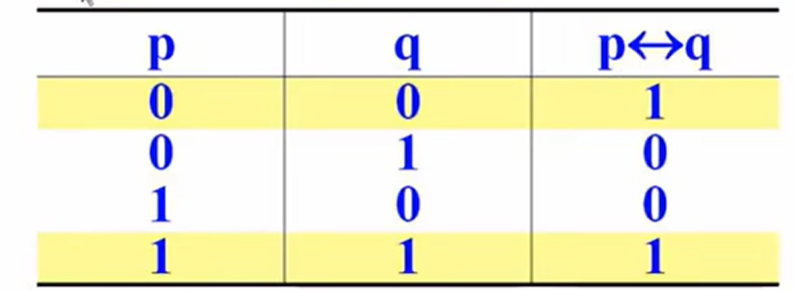
五大联结词真值表
| p | q | $ \neg p $ | $ p \wedge q $ | $ p \vee q $ | $ p \rightarrow q $ | $p \leftrightarrow q$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
哑元
命题中命题变元的取值对于命题的真值没有影响的命题变元称为哑元。
现在有一下四个命题：
- $p\rightarrow q$
- $ \neg p \vee r$
- $(\neg p \vee q) \rightarrow ((p\wedge r) )$
- $(q\rightarrow r) \wedge (p\rightarrow p)$
| p | q | r | $p\rightarrow q$ | $ \neg p \vee r$ | $(\neg p \vee q) \rightarrow ((p\wedge r) )$ | $(q\rightarrow r) \wedge (p\rightarrow p)$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
从命题不难看出$r$是公式 1 的哑元，$q$是公式 2 的哑元。对于公式 3 发现与公式 1 真值表一样，故$r$也是公式 3 的哑元，同理$q$也是公式 4 的哑元。
等值演算
等值式 $A \Leftrightarrow B$, $A \leftrightarrow B$ 是永真式。
例
判断$p \to q $ 和 $ \neg p \vee q $是否等值
列出真值表
| p | q | $p \to q $ | $\neg p \vee q$ | $p \to q \leftrightarrow \neg p \vee q$ |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
故 $p \to q \Leftrightarrow \neg p \vee q$
基本等值式
用真值表的方式来判断对于机器来说是或许是好方法，但是人显然不行，于是有一下 16 个基本等值式，以他们为基础进行演算，可以证明公式等值。
1.幂等律
$$ A \Leftrightarrow A \wedge A \Leftrightarrow A \vee A $$
2.交换律
$$ A \vee B \Leftrightarrow B \vee A, A \wedge B \Leftrightarrow B \wedge A$$
3.结合律
$$ A \vee B \vee C \Leftrightarrow A \vee \left ( B \vee C \right ) $$
$$ A \wedge B \wedge C \Leftrightarrow A \wedge \left (B \wedge C \right ) $$
4.分配律
$$ A \vee \left ( B\wedge C \right ) \Leftrightarrow \left (A \vee B \right ) \wedge \left ( A\vee C \right ) $$
$$ A \wedge \left ( B\vee C \right ) \Leftrightarrow \left (A \wedge B \right ) \vee \left ( A\wedge C \right ) $$
5.德摩根律
$$ \neg \left ( A\wedge B \right ) \Leftrightarrow \neg A\vee \neg B $$
$$ \neg \left ( A\vee B \right ) \Leftrightarrow \neg A\wedge \neg B $$
6.吸收律
$$ A \Leftrightarrow A\vee \left ( A\wedge B \right ) $$
$$ A \Leftrightarrow A \wedge \left ( A\vee B \right ) $$
7.零律
$$A\vee 1\Leftrightarrow 1, A\wedge 0\Leftrightarrow 0$$
8.排中律
$$ A\vee \neg A\Leftrightarrow 1 $$
9.矛盾律
$$ A\wedge \neg A\Leftrightarrow 0 $$
10.同一律
$$A \vee 1 \Leftrightarrow 1, A \wedge 0 \Leftrightarrow 0$$
11.双重否定律
$$A\Leftrightarrow \neg \neg A$$
12.蕴涵等值式
$$A \rightarrow B \Leftrightarrow \neg A \vee B$$
13.等价等值式
$$A \leftrightarrow B \Leftrightarrow (A \rightarrow B) \wedge(B \rightarrow A)$$
14.假言易位
$$A \rightarrow B \Leftrightarrow \neg B \rightarrow \neg A$$
15.等价否定等值式
$$A \leftrightarrow B \Leftrightarrow \neg A \leftrightarrow \neg B$$
16.归谬论
$$(A \rightarrow B) \wedge (A \rightarrow \neg B) \Leftrightarrow \neg A$$
置换规则
设 $ \Phi (A) $ 是含$A$的命题公式，$ \Phi (B) $ 是使用命题公式$B$的置换$ \Phi (A) $中的$A$，若$A \Leftrightarrow B$，则$ \Phi (A) \Leftrightarrow \Phi (B)$。
例如，试证明 $(p \vee q) \rightarrow r \Leftrightarrow (p \rightarrow r) \wedge (q \rightarrow r)$
解：
$$(p \rightarrow r) \wedge (q \rightarrow r)$$
$$\Leftrightarrow (\neg p \vee r) \wedge (\neg q \vee r) (蕴涵等值式)$$
$$\Leftrightarrow \neg (p \vee q) \vee r(德摩根律，分配律)$$
$$\Leftrightarrow (p \vee q) \rightarrow r(蕴涵等值式)$$
范式
命题变项及其否定统称作文字。仅由有限个文字的析取式称作简单析取式。仅由有限个文字的合取式称作简单合取式。仅由有限个简单析取式的合取构成的命题公式称作合取范式。仅由有限个简单合取式的析取构成的命题公式称作析取范式。
一个简单析取式是重言式当且仅当它同时含有某个命题变项和它的否定式。一个简单合取式是矛盾式当且仅当它同时含有某个命题变项和他的否定式。
一个析取范式是矛盾式当且仅当它每个简单合取式是矛盾式.一个合取范式是重言式当且仅当他的每个简单析取式是重言式。
任何命题公式都存在与之等值的析取范式和合取范式。
试着求下面的命题公式的合取范式和析取范式
$$(p \rightarrow q) \leftrightarrow r$$
- 合取范式
$$(p \rightarrow q) \leftrightarrow r$$
$$\Leftrightarrow (\neg p \vee q) \leftrightarrow r，消去\rightarrow$$
$$\Leftrightarrow ((\neg p \vee q) \rightarrow r) \wedge (r \rightarrow (\neg p \vee q))，消去\leftrightarrow$$
$$\Leftrightarrow (\neg (\neg p \vee q) \vee r) \wedge (\neg r \vee (\neg p \vee q))，消去\rightarrow$$
$$\Leftrightarrow ((p \wedge \neg q) \vee r) \wedge (\neg r \vee \neg p \vee q)，德摩根律否定内移$$
$$\Leftrightarrow (p \vee r) \wedge (\neg q \vee r) \wedge (\neg r \vee \neg p \vee q)，分配律$$ - 析取范式
$$(p \rightarrow q) \leftrightarrow r$$
$$\Leftrightarrow ((p \wedge \neg q) \vee r) \wedge (\neg r \vee \neg p \vee q)$$
$$\Leftrightarrow (p \wedge \neg q \wedge \neg r)\vee (\neg p \wedge r)\vee (q \wedge r)$$
主范式
在含有 n 个命题变项的简单合取式（简单析取式）中，若每个命题变项和他的否定式敲好出现一个且仅出现一次，而命题变项或者它的否定式按照字典西排列，这样的简单合取式（简单析取式）称为极小项（极大项）
极小项
| 公式 | 成真赋值 | 名称 |
|---|---|---|
| $\neg p\wedge \neg q\wedge \neg r$ | 0 0 0 | $m_0$ |
| $\neg p\wedge \neg q\wedge r$ | 0 0 1 | $m_1$ |
| $\neg p\wedge q\wedge \neg r$ | 0 1 0 | $m_2$ |
| $\neg p\wedge q\wedge r$ | 0 1 1 | $m_3$ |
| $p\wedge \neg q\wedge \neg r$ | 1 0 0 | $m_4$ |
| $p\wedge \neg q\wedge r$ | 1 0 1 | $m_5$ |
| $p\wedge q\wedge \neg r$ | 1 1 0 | $m_6$ |
| $p\wedge q\wedge r$ | 1 1 1 | $m_7$ |
极大项
| 公式 | 成假赋值 | 名称 |
|---|---|---|
| $p\vee q\vee r$ | 0 0 0 | $M_0$ |
| $p\vee q\vee \neg r$ | 0 0 1 | $M_1$ |
| $p\vee \neg q\vee r$ | 0 1 0 | $M_2$ |
| $p\vee \neg q\vee \neg r$ | 0 1 1 | $M_3$ |
| $\neg p\vee q\vee r$ | 1 0 0 | $M_4$ |
| $\neg p\vee q\vee \neg r$ | 1 0 1 | $M_5$ |
| $\neg p\vee \neg q\vee r$ | 1 1 0 | $M_6$ |
| $\neg p\vee \neg q\vee \neg r$ | 1 1 1 | $M_7$ |
极大项和极小项还有一下关系：$\neg m_i \Leftrightarrow M_i$
由都是极大项或者极小项组成的范式称为主范式，对于一个命题主范式唯一。
前文已经求过命题公式$(p \rightarrow q) \leftrightarrow r$ 的析取范式和合取范式
析取范式：
$$(p \wedge \neg q \wedge \neg r)\vee (\neg p \wedge r)\vee (q \wedge r)$$
合取范式：
$$(p \vee r) \wedge (\neg q \vee r) \wedge (\neg r \vee \neg p \vee q)$$
求主析取范式：
可以发现在析取范式的后两项并没有包含全部元素，可以通过$A \wedge1$的方式填补，即：
$$\neg q \wedge r$$
$$\Leftrightarrow \neg p \wedge (\neg q \vee q) \wedge r$$
$$\Leftrightarrow (\neg p \wedge \neg q \wedge r) \vee (\neg p \wedge q \wedge r)$$
$$\Leftrightarrow m_1 \vee m_3$$
$$q \wedge r$$
$$\Leftrightarrow (\neg p \vee p) \wedge q\wedge r$$
$$\Leftrightarrow (\neg p\wedge q\wedge r) \vee(p\wedge q\wedge r)$$
$$\Leftrightarrow m_3\vee m_7$$
$$(p \wedge \neg q \wedge \neg r)\vee (\neg p \wedge r)\vee (q \wedge r)$$
$$\Leftrightarrow (p \wedge \neg q \wedge \neg r) \vee (\neg p \wedge \neg q \wedge r) \vee (\neg p \wedge q \wedge r)\vee (\neg p\wedge q\wedge r) \vee(p\wedge q\wedge r)$$
$$\Leftrightarrow m_1\vee m_3\vee m_7$$
类似的原理求主合取范式可以通过在缺项的简单析取式中通过$A \vee 0$的方式来填补，可以求得：
$$(p \rightarrow q) \leftrightarrow r \Leftrightarrow M_0\wedge M_2\wedge M_5\wedge M_6$$
联结词完备集
在认识联结词完备集之前，我们首先要认识什么是n 元真值函数。
称$F:{0,1}^n \rightarrow {0,1}$为n 元真值函数。在这个定义中，F 的自变量为 n 个命题变项，定义域${0,1}^n={00…0,00…1,…,11…1}$，即由 01 组成的长度为 n 的符号串整体，值域为${0,1}$
一元真值函数：
| p | $F^1_0$ | $F^1_1$ | $F^1_2$ | $F^1_4$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
二元真值函数:
| p | q | $F^2_0$ | $F^2_1$ | $F^2_2$ | $F^2_3$ | $F^2_4$ | $F^2_5$ | $F^2_6$ | $F^2_7$ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| p | q | $F^2_8$ | $F^2_9$ | $F^2_10$ | $F^2_11$ | $F^2_12$ | $F^2_13$ | $F^2_14$ | $F^2_15$ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
设 S 是联结词完备集，如果任何 n(n>=1)元真值函数都可以由仅含 S 中的联结词构成的公式表示，则成 S 是联结词完备集。
这样很容易得到一个定理，即$S={\neg,\vee,\wedge}$是联结词完备集，因为任何一个主析取范式和主合取范式都可以由这三个构成。
根据这个定理，我们发现 $\wedge$ 可以用 $\neg,\vee$ 表示， $\vee$ 也可以用 $\neg,\wedge$ 表示，故${\neg,\vee}$,${\neg,\wedge}$也是联结词完备集。
这样很容易得到证明联结词集是否是联结词完备集的思路，就是看联结词能不能表示$\neg$,和$\vee,\wedge$二选一。
可满足性问题与消解法
不含任何文字的简单析取式称为空简单析取式，记作 λ。规定 λ 是不可满足的。
约定:简单析取式不能同时含有一个命题变项和它的否定。
$S\approx S^t$,S 可满足当且仅当$S^t$可满足
设$C_1,C_2$是两个简单析取式,$C_1$含文字$l$,$C_2$含文字$l^c$(文字$l$的补集)，即$C_1=C^t_1 \vee l, C_2=C^t_2\vee l^c$，将文字$l$删去在析取成一个简单析取式，称这样的结果为$C_1,C_2$的消解式或者消解结果，记作$Res(C_1,C2)$, $Res(C_1,C2) = C^t_1 \vee C^t_2$。
一个定理：$C_1^t \wedge C_2^t \approx Res(C_1,C_2)$
设$S$是一个合取范式，$C_1,C_2…C_n$是一个简单析取式序列，$C_i$是$S$中的一个简单析取式或者是这些简单析取式的消解结果，则称该序列为由 S 导出的结果$C_n$的消解序列，若$C_n$为 λ 则称此序列为 S 的一个否证。若合取范式 S 是不可满足的，则 S 有否证，当且仅当有否证。
逻辑推理
设$A_1,A_2,…,A_k$和$B$都是命题公式，若对于$A_1,A_2,…,A_k$和$B$中出现的命题变项的任意一组赋值，或者$A_1\wedge A_2\wedge…\wedge A_k$为假，或者$A_1\wedge A_2\wedge…\wedge A_k$为真时$B$也为真，则称前提$A_1,A_2,…,A_k$推出结论$B$是有效的，并称$B$为有效的结论。
